12 Hypothesis test concerning TWO population parameters
In order to test difference between two population parameters we need to draw samples from two populations. Using sample statistics and appropriate test statistics we can test whether there is any significant difference between the parameters of interest. In this chapter we will discuss:
1) testing difference between two population means;
2) testing difference between two population variances;
3) testing difference between two means from matched pairs experiment;
4) testing difference between two population proportions.
12.1 Hypothesis test: Difference between two population means (\(\mu_1-\mu_2\))
Assumptions:
The two samples must be independent of each other.
The populations from which the samples are drawn should be normally distributed, especially when the sample size is small (typically \(n<30\)).
With larger samples, the Central Limit Theorem justifies the use of normal approximation even if the population is not normal.
12.1.1 Case-I: When \(\sigma_1^2\) and \(\sigma_2^2\) are known
To test \(H_0: \mu_1-\mu_2=D_0\) the test statistic is:
\[ z=\frac{(\bar x_1-\bar x_2)-D_0}{s.e(\bar x_1-\bar x_2)}=\frac{(\bar x_1-\bar x_2)-D_0}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma^2_2}{n_2}}} \tag{12.1}\]
The test-statistic z follows standard normal distribution. The rejection rule of \(H_0\) is same as one-sample z-test.
Problem 12.1 Consider the following information:
| Sample 1 | Sample 2 |
|---|---|
| \(n_1=80\) | \(n_1=70\) |
| \(\bar x_1=104\) | \(\bar x_2=106\) |
| \(\sigma_1=8.4\) | \(\sigma_2=7.6\) |
Now test the following hypothesis:
\[ H_0: \mu_1-\mu_2=0 \]
\[ H_1:\mu_1-\mu_2\ne 0 \]
Problem 12.2 (Larson and Farber 2015)A credit card watchdog group claims that there is a difference in the mean credit card debts of households in California and Illinois. The results of a random survey of 250 households from each state are shown at the bottom. The two samples are independent. Assume that \(\sigma_1 =\$ 1045\) for California and \(\sigma_2=\$1350\) for Illinois. Do the results support the group’s claim? Use \(\alpha= 0.05\).
| California | Illinois |
|---|---|
| \(\bar x_1=\$ 4777\) | \(\bar x_2=\$ 4866\) |
| \(n_1=250\) | \(n_2=250\) |
Problem 12.3 (Larson and Farber 2015) A travel agency claims that the average daily cost of meals and lodging for vacationing in Alaska is greater than the average daily cost in Colorado. The table at the bottom shows the results of a random survey of vacationers in each state. The two samples are independent. Assume that \(\sigma_1=\$24\) for Alaska and \(\sigma_2=\$19\) for Colorado, and that both populations are normally distributed. At \(\alpha= 0.05\), is there enough evidence to support the claim?
| Alaska | Colorado | |
|---|---|---|
| Sample mean | $ 296 | $ 293 |
| Sample size | 15 | 20 |
12.1.2 Case-II(A): \(\sigma_1^2\) and \(\sigma_2^2\) are unknown but equal(\(\sigma_1^2=\sigma_2^2\))
To test \(H_0: \mu_1-\mu_2=D_0\) the test statistic is:
\[ t=\frac{(\bar x_1-\bar x_2)-D_0}{\sqrt {s^2_p(\frac{1}{n_1}+\frac{1}{n_2})}} \tag{12.2}\]
Here, \(s^2_p\) is the pooled variance and
\[ s^2_p=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2} \]
The test statistic t follows the Student t distribution with \(df=n_1+n_2-2\). The rejection rule of \(H_0\) is same as one-sample t-test.
12.1.3 Case-II(B): \(\sigma_1^2\) and \(\sigma_2^2\) are unknown and NOT equal(\(\sigma_1^2 \ne\sigma_2^2\))
To test \(H_0: \mu_1-\mu_2=D_0\) the test statistic is:
\[ t=\frac{(\bar x_1-\bar x_2)-D_0}{\sqrt{( \frac{s_1^2}{n_1}+\frac{s^2_2}{n_2}} )} \tag{12.3}\]
with \(df=\frac{(s_1^2/n_1+s_2^2/n_2)^2}{\frac{(s_1^2/n_1)^2}{n_1-1}+\frac{(s_2^2/n_2)^2}{n_2-1} }\)
12.2 Testing the Population Variances (\(\sigma_1^2=\sigma^2\))
The hypothesis to test the equality of two population variances is:
\[ H_0: \sigma_1^2=\sigma_2^2 \]
\[ H_1: \sigma_1^2\ne\sigma_2^2 \]
Test statistic
\[ F=\frac{s_1^2}{s_2^2} \tag{12.4}\]
The \(F\)-statistic is \(F\)-distributed with degrees of freedom \(\nu_1=n_1-1\) and \(\nu_2=n_2-1\).
Assuming \(s_1^2>s_2^2\) ,we can reject the \(H_0\) if \(F>F_{\alpha/2, \nu_1,\nu_2}\) ( Here \(\alpha/2\) is the area in the upper tail).
NOTE: We refer to the population providing the larger sample variance as population 1 .
Problem 12.4 The following data were collected from two population- population A and population B.
| Population A | Population B | |
|---|---|---|
| Sample size | 35 | 40 |
| Sample mean | 13.6 | 10.1 |
| Sample variance | 5.2 | 8.5 |
a) Test the equality of variances of the two populations at \(\alpha=5\%\).
Solution (a):
Since the sample variance of population B is greater than that of population A; we consider population B as population 1.
So, \(s_1^2=8.5 , s_2^2=5.2\) and \(n_1=40; n_2=35\)
We have to test the following hypothesis :
\[ H_0: \sigma_1^2=\sigma_2^2 \]
\[ H_1: \sigma_1^2\ne\sigma_2^2 \]
Test statistic:
\[ F=\frac{s_1^2}{s_2^2}=\frac{8.5}{5.2}=1.635 \]
Critical value: For \(\alpha/2=0.025\)
\[ F_{0.025,39,34}\approx1.93 \]
Decision: Since \(F \ngtr F_{\alpha/2}\); so we cannot reject the \(H_0\). So the the equality assumption of the two population variances are met.
b) Then use appropriate test statistic to test equality of two population means at \(\alpha=5\%\).
Solution (b):
We have to test the following hypothesis:
\[ H_0: \mu_1-\mu_2=0 \]
\[ H_1: \mu_1-\mu_2\ne 0 \]
Since equality of population variance is fulfilled so the appropriate test statistic is :
\[ t=\frac{(\bar x_1-\bar x_2)}{\sqrt {s^2_p(\frac{1}{n_1}+\frac{1}{n_2})}} \]
Where, \[ s^2_p=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}=6.963014 \]
So, \(t=\frac{10.1-13.6}{\sqrt{6.963014(\frac{1}{40}+\frac{1}{35})}}=-5.731\)
Critical value: At \(\alpha/2=0.025\) , with \(df=40+35-2=73\)
\(-t_{\alpha/2}\approx -1.992\)
Decision: Since the value of \(t\) false in the rejection region (RR) we can reject the \(H_0\) .
Conclusion: With 95% confidence we can conclude that the population means are not equal; rather mean of population 1 (B) is significantly lower than the mean of population 2 (A).
Problem 12.5 An accounting firm is interested in providing opportunities for its auditors to gain more expertise in statistical sampling methods. They wish to compare traditional classroom instruction with online self-paced tutorials. Auditors were assigned at random to one type of instruction, and the auditors were then given an exam. The table shows how the two groups performed.
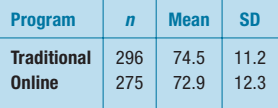
a) Test equality of variances of two methods of learning.
b) Test whether there is any significant difference in mean scores between Traditional and Online method.
12.3 Hypothesis test: Comparing TWO means when the samples are dependent/ matched/paired
The paired t-test is used to compare the means of two related groups (e.g., before-and-after measurements on the same subjects). To validly apply the test, the following assumptions must be met:
Assumptions of the Paired t-test:
Paired observations: Each subject or entity provides a pair of observations (e.g., pre-treatment and post-treatment). The test assumes that data are dependent.
Continuous or interval scale: The differences between paired observations should be measured on a continuous (interval or ratio) scale.
Normality of the differences:
The distribution of the differences (not the raw values) between the paired observations should be approximately normally distributed.
For small samples (typically n < 30), this assumption is critical.
For larger samples, the Central Limit Theorem provides robustness.
- No significant outliers in the differences:
Extreme outliers in the differences can heavily influence the result and violate the normality assumption.
Test procedure
Suppose \(n\) subjects are measured in two different occasion/conditions regarding the measurement variable \(X\).
Let, \(\mu_A\) be the population mean of \(X\) under condition A and
\(\mu_B\) be the population mean of \(X\)under condition B
So the difference between the means is \(\mu_d=\mu_A-\mu_B\)
To test the hypotheses:
\[ H_0: \mu_d=0 \]
\[ H_1: \mu_d \ne 0 \]
the test statistic is:
\[ t=\frac{\bar d -\mu_d}{s_d/ \sqrt{n} } \]
which is Student t distributed with \(n-1\) degrees of freedom, provided that the differences are normally distributed.
The rejection rule is similar as one-sample t-test.
Here,
\(n=\) sample size
\(d_i=\) difference in measurements between two conditions from \(i^{th}\) subject
\[\bar d=\frac{\sum_{i=1}^{n} d_i}{n}\]
\[s_d=\sqrt { \frac{\sum_{i=1}^{n} (d-\bar d)^2}{n-1}}\]
Problem 12.6 (Black 2012, 10.27)
Eleven employees were put under the care of the company nurse because of high cholesterol readings. The nurse lectured them on the dangers of this condition and put them on a new diet. Shown are the cholesterol readings of the 11 employees both before the new diet and one month after use of the diet began.
| Employee | Before | After |
|---|---|---|
| 1 | 255 | 197 |
| 2 | 230 | 225 |
| 3 | 290 | 215 |
| 4 | 242 | 215 |
| 5 | 300 | 240 |
| 6 | 250 | 235 |
| 7 | 215 | 190 |
| 8 | 230 | 240 |
| 9 | 225 | 200 |
| 10 | 219 | 203 |
| 11 | 236 | 223 |
Use \(\alpha=0.05\) to test for a significant difference between population means for the before and after cholesterol readings.
Solution:
Let, \(\mu_B\) be the population of cholesterol readings before nurse’s lecture and
\(\mu_A\) be the population of cholesterol readings after nurse’s lecture.
The difference is : \(\mu_A-\mu_B=\mu_D\)
Hypotheses:
\[ H_0: \mu_D=0 \]
\[ H_1: \mu_D\ne 0 \]
Required calculation for test of hypotheses
| Employee | Before | After | Difference, \(d=After-Before\) |
|---|---|---|---|
| 1 | 255 | 197 | -58 |
| 2 | 230 | 225 | -5 |
| 3 | 290 | 215 | -75 |
| 4 | 242 | 215 | -27 |
| 5 | 300 | 240 | -60 |
| 6 | 250 | 235 | -15 |
| 7 | 215 | 190 | -25 |
| 8 | 230 | 240 | 10 |
| 9 | 225 | 200 | -25 |
| 10 | 219 | 203 | -16 |
| 11 | 236 | 223 | -13 |
Using calculator;
\(\sum d=-309\)
\(\bar d= \frac{\sum d}{n}=\frac{-259}{11}=-28.09\)
\(s_D=\sqrt \frac{\sum d^2-n(\bar d)^2}{n-1}=25.81\)
Test statistic
\[ t=\frac{\bar d-\mu_D}{s_D/\sqrt n}=\frac{-28.09-0}{25.81/\sqrt 11}=-3.609 \]
Critical value
For\(\alpha=0.05\) and \(df=n-1=11-1=10\);
\[ -t_{\alpha/2}=t_{0.025}=-2.228 \]
Since \(t\) falls in CR (\(t<-t_{\alpha/2}\)), so reject \(H_0\).
Hence we can conclude with 95% confidence that the cholesterol reading before and after nurse’s lecture are not same; actually after lecture mean cholesterol reading was decreased.
Problem 12.7 (Lind, Marchal, and Wathen 2012) Advertisements by Sylph Fitness Center claim that completing its course will result in losing weight. A random sample of eight recent participants showed the following weights before and after completing the course. At the 0.01 significance level, can we conclude the students lost weight?
| Name | Before | After |
|---|---|---|
| Hunter | 155 | 154 |
| Cashman | 228 | 207 |
| Mervine | 141 | 147 |
| Massa | 162 | 157 |
| Creola | 211 | 196 |
| Peterson | 164 | 150 |
| Redding | 184 | 170 |
| Poust | 172 | 165 |
Solution:
Let, \(\mu_B=\) pop. mean of weight before completing the course
\(\mu_A=\) pop. mean of weight after completing the course
According to the claim ; \(\mu_A<\mu_B\) that is \(\mu_A-\mu_B<0 \implies \mu_D<0\). So the
Hypotheses
\[ H_0: \mu_D\ge 0 \]
\[ H_1: \mu_D<0 \]
Do it yourself the rest of the calculation………………………
[Ans: \(\bar d= -8.875; s_D=8.774; t=-2.861, -t_{\alpha}=-1.895\) . Reject \(H_0\). ]
Problem 12.8 (Lind, Marchal, and Wathen 2012) The management of Discount Furniture, a chain of discount furniture stores in the Northeast, designed an incentive plan for salespeople. To evaluate this innovative plan, 12 salespeople were selected at random, and their weekly incomes ($) before and after the plan were recorded.
| Salesperson | Before | After |
|---|---|---|
| Sid Mahone | 320 | 340 |
| Carol Quick | 290 | 285 |
| Tom Jackson | 421 | 475 |
| Andy Jones | 510 | 510 |
| Jean Sloan | 210 | 210 |
| Jack Walker | 402 | 500 |
| Peg Mancuso | 625 | 631 |
| Anita Loma | 560 | 560 |
| John Cuso | 360 | 365 |
| Carl Utz | 431 | 431 |
| A. S. Kushner | 506 | 525 |
| Fern Lawton | 505 | 619 |
Was there a significant increase in the typical salesperson’s weekly income due to the innovative incentive plan? Use the 0.05 significance level.